

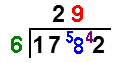
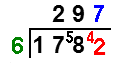

Arabic Numbers --- Introduction --- Add --- Subtract --- Multiply --- Divide --- Practise sums --- Less than 1 --- Types of numbers
If you want to practise your mental arithmetic at division, click here.
Divide is sometimes also known as over or of. You can say two over three to mean two divided by three, or one of four to mean one divided by four.
Division is the opposite of multiplication. If you want to divide this number by that number, you can work it out by thinking "What number multiplied by that number gives this number?"
Division is not commutative. 2/3 is different from 3/2. It is not associative. (10/2)/5=1 but 10/(2/5)=25. It is only sometimes distributive over addition and subtraction. (2+3)/6 = 2/6 + 3/6 but 6/(2+3) = 6/5 while 6/2 + 6/3 = 3 + 2 = 5.
With addition, subtraction and multiplication, you end up with a single answer. With division, if you are dealing with whole numbers, you may end up with a remainder. If you want to divide 17 pieces of chocolate between 5 people, then they can have 3 pieces each, and 2 are left over. These are the remainder, or as a young child once said, "3 pieces of chocolate each, and an argument"! There is another way of doing division, where you can end up with a fractional answer.
Here is how you can divide a single digit into a longer number.
| We want to divide 6 into 1782. You write the longer number, 1782, with a line above and to the left. You write the single digit, 6, to the left of this. |  |
| Now to start the calculation. You divide 6 into the first bit of the longer number. 6 into 1 won't go, so you try the next digit as well. 6 into 17 goes 2 remainder 5. You put the 2 above the end of the 17, and write the 5 in front of the next digit 8. This is a carry. It makes 58. |  |
| 6 into 58 goes 9 remainder 4. You write the 9 in the answer, and carry the 4. | 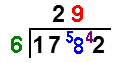 |
| Now 6 into 42 goes 7 with no remainder, so we have a complete answer 297. | 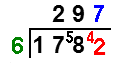 |
If there had been a remainder at the end, either we would give it as part of the answer, or we would put a decimal point at that point in the answer, and carry on doing the division with the (implied) zeroes after the decimal point.
Click on Get sum for some practice in division. When the sum appears, enter the answer in the boxes. There are boxes provided for carries, but you don't have to use them.
Long division is where both numbers are bigger. It is is much more complicated. The remainder may be several digits long. It is harder to calculate, and you won't be able to write it next to the next digit, as there won't be room. So you do all this working underneath, instead. Click on Get sum for a demonstration. You will get different numbers each time.
You can see how we write down the multiple of the dividend (the number which is doing the dividing into) underneath the divisor (the number being divided). The example explains what the multiple is, but you don't need to write this. Then we subtract them to get the remainder. The next digit gets brought down (the black lines indicate this, you don't need to write this either!) and you carry on. It's the same technique as above, but laid out clearer.
One problem with this technique is that you need to work out these multiples. I remember making a guess, then doing scruffy calculations on scrap paper to see if I was right. However, Napier's bones would be very useful for this.
A number like 18 has several factors. These are numbers that divide into it without a remainder. So both 2 and 3 are factors of 18. Factors tend to come in pairs: 2 x 9 = 18, so both 2 and 9 are factors. The only factors without a pair are for squares. 5 x 5 = 25, so 5 is a factor of 25, but doesn't have a pair. All numbers have at least two factors, as all numbers can be divided by 1 and themselves. If these are the only 2 factors, then it is a prime number.
If a number has 2 as a factor, then it is an even number. (All other numbers are odd.)
There are tricks to find some factors:
| Factor | Trick | Example | ||
|---|---|---|---|---|
| Number | What to do | Factors | ||
| 2 | If the last digit of the number is even then the whole number divides by 2. |
296 | 4 is even | 2 x 148 |
| 3 | Add up the digits of the number. If this divides by 3, so is the number. |
174 | 1 + 7 + 4 = 12 which divides by 3 | 3 x 58 |
| 4 | If the last two digits divide by 4 then so does the whole number. |
144 | 44 divides by 4 | 4 x 36 |
| 5 | If the last digit is 5 or 0 the number divides by 5. |
535 | last digit is 5 | 5 x 107 |
| 6 | Work out if number divides by 2 and 3. | 630 | last digit is 0 6 + 3 + 0 = 9 | 6 x 105 |
| 8 | If the last three digits divide by 8 then so does the whole number. |
3816 | 816 divides by 8 | 8 x 477 |
| 9 | Add up the digits of the number. If this divides by 9, so is the number. |
882 | 8 + 8 + 2 = 18 which divides by 9 | 9 x 98 |
| 10 | If the last digit is 0 the number divides by 10. |
480 | last digit is 0 | 10 x 48 |
| 11 | Add up alternate digits and subtract them. If result divides by 11 (or is 0), the number divides by 11. |
8162 | 8 + 6 = 14 1 + 2 = 3 14 - 3 = 11 | 11 x 742 |
| 12 | Work out if number divides by 3 and 4. | 432 | 4 + 3 + 2 = 9 32 is divisible by 4 | 12 x 36 |
You may notice that there is no trick for 7. In fact, there is one, but it is so complicated that I think a bit of short division for short numbers, or a calculator for long numbers, would be easier! But if you're interested, here you are. This rule is called L-2M. What you do is to double the last digit of the number X and subtract it from X without its last digit. For instance, if the number X you are testing is 345678, you would subtract 16 from 34567. Repeat this procedure until you get a number that you know for sure is or is not divisible by seven. Then the X's divisibility will be the same.
Slide rules were used up to the 1970's for quick division, although they gave imprecise answers.
Now, of course, everyone uses calculators.
However, it's best to make sure that you can do simple sums in your head. Click here to learn to do mental arithmetic quickly and accurately!
© Jo Edkins 2006 - Return to Numbers index