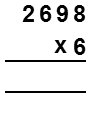
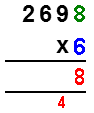




Arabic Numbers --- Introduction --- Add --- Subtract --- Multiply --- Divide --- Practise sums --- Less than 1 --- Types of numbers
If you want to practise your mental arithmetic at multiplication, click here.
Multiply is sometimes also known as times.
Here are the multiplication tables laid out for you to look at. Click on numbers at the top and the side.
You can spot patterns in these tables, which means that there is less to learn.
Multiplication is commutative, as 2x3 = 3x2. It is also associative, as 2x(3x4)=(2x3)x4. Multiplication is also distributive over both addition and subtraction. This means that a(b+c)=ab+ac, and a(b-c)=ab-ac.
For example: 2 x (3 + 5) = 2 x 8 = 16 and 2 x 3 + 2 x 5 = 6 + 10 = 16
For example: 7 x (4 - 2) = 7 x 2 = 14 and 7 x 4 - 7 x 2 = 28 - 14 = 14
When you see a calculation with addition, subtraction, multiplication and division, you need to decide what order to do the calculation. 1+2x3 can do interpreted as (1+2)x3 which gives the answer 9, or 1+(2x3) which is 7. Simple calculators do the calculations from left to right, so give the answer 9. However, mathematicians have decided on a different order. They do anything inside brackets before aything else. Then they do division and multiplication. Finally they do addition and subtraction. So with 1+2x3, the 2x3 is done first, giving 6 and then the one is added afterwards, giving 7. This order is called BODMAS.
| B | - Brackets |
|---|---|
| O | - perhaps Of (meaning division) |
| D | - Division |
| M | - Multiplication |
| A | - Addition |
| S | - Subtraction |
Scientific calculators use this order. So does this arithmetic calculator. If you write down a formula for someone else to use, and you're not sure if they understand what order to do the calculation, then put in extra brackets to make sure!
Here is how you multiply on paper rather than using a calculator.
| This example multiplies a long number 2698 by a single digit 6. You write the long number, then the single digit underneath, then draw two lines under that. | 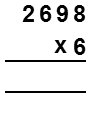 |
| Now you start the calculation. You multiply the last digit of the long number, which is 8, by 6. This gives 48. You write the units of this, the 8, between the lines in the end column. You write the tens, the 4, under the bottom line in the next column. This is called carrying the 4 forward. You can see that the red numbers do give 48. | 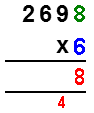 |
| Now you move onto the next digit in the longer number, 9. If you multiply 9 by 6, you get 54. But you must also add the 4 which was carried forward. So you have 58. The 8 goes between the line and the 5 is carried forward. |  |
| The next digit in the longer number is 6. You will have worked out by now that the digit we are working on is green! 6 x 6 = 36. Add 5 which was carried forward last time. You get 41 - 1 in the answer, and 4 to carry forward. |  |
| Finally we multiply the first digit of the larger number, 2 by 6. This gives 12. Add the carry, 4, to give 16. No need to carry anything as we have finished the calculation, so just write 16 down. There is the answer 16188. |  |
Click on Get sum for some practice in multiplication. When the sum appears, enter the answer in the boxes. There are boxes provided for carries, but you don't have to use them.
Long multiplication, where you multiply two long numbers together, is more complicated. It depends on the fact that you can split a long number up into single digits.
234 = 2 x 100 + 3 x 10 + 4
So you can multiply a number by 234 by first multiplying it by 2 x 100, then 3 x 10, then 4, and then adding these together. Does this help? Yes, it does, because you can easily multiply by ten or a hundred. To multiply by ten, add a zero on the end of a number. To multiply by a hundred, add 2 zeroes, and so on.
Click on Get sum for a demonstration of how long multiplication works You will get different numbers each time.
You have to learn your multiplication tables to do multiplication on paper, and it's a good idea to learn them anyway, as simple multiplications come up all the time, in mathematics or in life, and it's much quicker to do them in your head. Most people find that they know their simple tables all right, but get confused around six, seven, eight and nine times tables. Here is a way of doing your nine times table using your fingers, and here is a way to do your six, seven, eight or nine times table using your fingers.
There have been machines which do multiplication for centuries. John Napier, a clever mathematician, invented Napier's bones to do his multiplication for him, which makes me wonder how good he was at his multiplication tables! Slide rules were used up to the 1970's. Now, of course, everyone uses calculators.
However, it's best to make sure that you can do simple sums in your head. Click here to learn to do mental arithmetic quickly and accurately!
© Jo Edkins 2006 - Return to Numbers index